北航微分几何讨论班（2021年春第7讲）
题目：Sharp affine isoperimetric inequalities for the volume decomposition functionals of polytopes
报告人：熊 革 教授（同济大学）
报告时间：2021.4.30 10:00-11:00
腾讯会议号：570 714 666
摘要：In this talk, I will introduce our very recent work on the geometry of polytopes. We prove that the nth power of the volume functional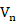 
of polytopes P in 
,
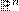according to dimensions of the spaces spanned by any n outer normal unit vectors of P, is naturally decomposed into n homogeneous polynomials with degree n. Several new sharp affine isoperimetric inequalities for these functionals are established, which essentially characterize the geometric and algebraic structures of polytopes.
报告人简介：熊革，同济大学教授、博士生导师。主要研究凸体几何。他解决了Lp 静电容量的Minkowski 问题；提出并证明了“Lp transference principle”，对Lp Brunn-Minkowski型不等式进行了统一处理。他解决了凸体几何中的几个公开问题，包括锥体积泛函仿射极值的Lutwak-Yang-Zhang公开问题的2，3维情形；由截面确定凸体的Baker-Larman公开问题的2维情形；完全解决了G. Zhang关于凸体的John 椭球与对偶惯性椭球的一致性问题。
他在国际纯数学重要期刊如JDG, AIM, JFA, CVPDE, IUMJ, IMRN, CAG, DCG等发表论文近30篇。他的研究成果或被写入凸体几何的经典教材中、或被发表在国际顶尖期刊上的文章多次引用和正面评价。
邀请人：张世金
