信赖域子问题局部解首次被揭示存在充分必要的最优性条件

日前，我校hjc888老品牌黄金城夏勇教授和2017级博士研究生王玖鳞在著名的信赖域子问题的局部非全局解的最优性条件刻画上取得重要进展，解决了该领域一个困扰27年的数学难题。研究成果“Closing the gap between necessary and sufficient conditions for local non-global minimizer of trust region subproblem”发表在《SIAM Journal on Optimization》，该期刊为数学优化领域权威期刊，2019年影响因子为2.247，期刊副主编认为该项工作是“对非线性规划文献的坚实贡献”（英文原文为“solid contribution to the nonlinear-programming literature”）。（论文链接：https://epubs.siam.org/doi/pdf/10.1137/19M1294459）

信赖域子问题是非线性优化中的著名问题，是经典信赖域算法求解无约束优化问题时每个迭代步都需要求解的子问题。其数学模型为在单位球上极小化一个（非凸）二次函数。

一般非凸信赖域子问题全局最优解的充分必要的最优性条件最早于1981年由美国桑迪亚国家实验室D.M.Gay建立。然而其局部最优解的最优性条件囿于一般非线性优化的经典分析框架。1994年，巴西科学院院士J.M.Martínez证明了信赖域子问题最多只有一个局部非全局解这一令人吃惊的结果，但该里程碑工作中所建立的局部非全局最优解的充分性条件与必要性条件之间仍有一个差距。该差距的存在引发人们的困扰，如D.C.优化领域著名学者P.D. Tao和L.T.H. An在1998年明确指出如下悖论：检验信赖域子问题的全局解比局部解更容易。

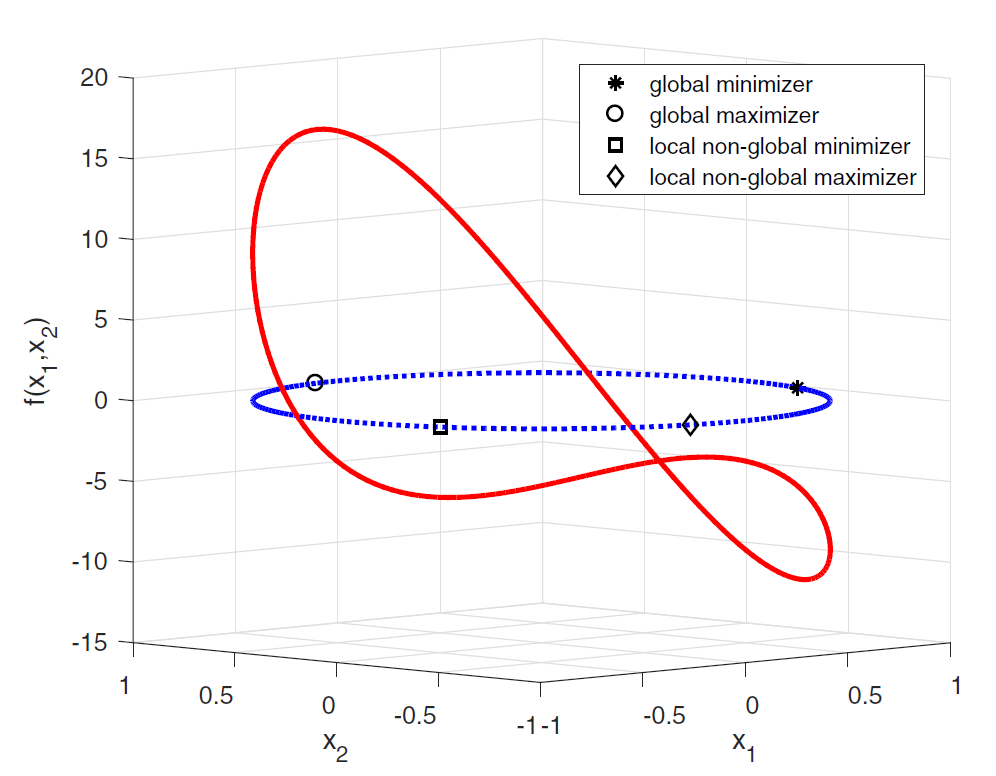
图1：二维空间信赖域子问题全局解和局部解示例

hjc888老品牌黄金城夏勇教授从2009年末接触该问题就被其所吸引并一直展开相关研究，2017级博士研究生王玖鳞从2015年做北航本科毕设起在夏勇教授指导下从事信赖域子问题的研究。2020年，他们取得了突破，首次建立了局部非全局解的充分必要的最优性条件，终结了信赖域子问题局部非全局解充分条件和必要条件之间存在了27年之久的这一间隙，首次证明局部非全局解亦可在多项式时间内可解，从而消除了信赖域子问题的Tao-An悖论。

至此，经过从1981年全局解到2020年局部非全局解四十年的努力，信赖域子问题局部解的最优性条件的理论刻画终于得到完全解决。

图2：论文首页部分截图

该项工作得到国家自然科学基金优秀青年科学基金、面上项目、北京市自然科学基金重点项目以及北京航空航天大学博士研究生卓越学术基金资助。