hjc888老品牌黄金城师生在国际顶级综合性数学杂志《Advances in Mathematics》发表研究成果

注：名字按照基础数学国际惯例，按照字母排序。第一作者：彭发，通讯作者：周渊 

2020年8月26日，国际顶级综合性数学杂志《Advances in Mathematics》在线刊登了hjc888老品牌黄金城2018级博士研究生彭发及其导师周渊等人在非线性退化方程研究方面的最新进展：《Hessian estimates for equations involving p-Laplacian via a fundamental inequality》。（论文链接：https://www.sciencedirect.com/science/article/pii/S0001870820302383）

他们在高维发现了一个基本的不等式，即对于任意光滑函数$v$, 总有下式成立：

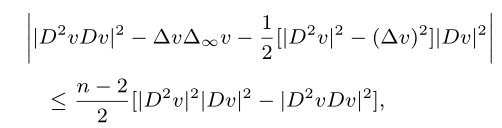
此不等式将Koch等人在平面上建立的等式推广到了高维空间，并且首次应用到了$p$-调和算子方面，在在平面上完全回答了Lindqvist等人提出的公开问题。此外，由于该不等式对含有$p$-拉普拉斯算子方程具有高度普适性，因此利用此不等式，能直接解决某类问题（如$p$-调和方程，带奇异项的$p$-拉普拉斯方程，抛物$p$-拉普拉斯方程，非齐次$p$-拉普拉斯类型方程）。总之，利用逼近观点和方程的结构，结合此不等式进行计算和求解，能得到前人未曾研究的结果。

Peter Lindavist 等人在2018年提出了下面的问题（即对于正规$p$-泊松抛物方程）：

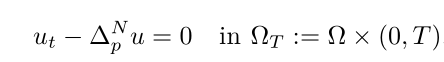
对于任意指标$p$属于1到无穷的开区间，其粘性解是否属于索伯列夫空间$W^{2,2}$—基于此问题，受Koch等人的工作启发，彭发等人在高维开发了新的不等式，并利用此不等式来尝试解决这个问题。在平面上，他们对此问题作出了正面的回答，在高维空间中，其得到的指标范围也优于Lindavist等人的工作。注意到，此方程在$Du=0$是退化的，所以研究其解的正则性，具有本质的困难。特别地，传统的方法Cordes条件，用来研究其解二阶正则性问题，具有一定的缺陷性。

共同参与工作的有：美国布朗大学 Hongjie Dong教授，瑞士苏黎世联邦理工大学Yi Ru-Ya Zhang教授。