北航数学论坛
报告题目:Spectral Decomposition and
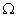 -Stability of Flows with Expanding Measures
-Stability of Flows with Expanding Measures
报告人:Keonhee Lee教授(韩国忠南国立大学)
报告时间:2018年12月14日下午3:00—4:00
报告地点:主213
报告摘要:In this talk we present a measurable version of the classical spectral decomposition theorem for flows. More precisely, we prove that if a flow
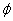 on a compact metric space
on a compact metric space
 is invariantly measure expanding on its chain recurrent set
is invariantly measure expanding on its chain recurrent set
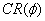 and has the invariantly measure shadowing property on
and has the invariantly measure shadowing property on
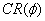 then
then
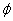 has the spectral decomposition, i.e. the nonwandering set
has the spectral decomposition, i.e. the nonwandering set
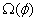 is decomposed by a disjoint union of finitely many invariant and closed subsets on which
is decomposed by a disjoint union of finitely many invariant and closed subsets on which
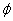 is topologically transitive. Moreover we show that if
is topologically transitive. Moreover we show that if
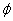 is invariantly measure expanding on
is invariantly measure expanding on
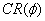 then it is invariantly measure expanding on
then it is invariantly measure expanding on
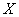 . Using this, we characterize the measure expanding flows on a compact
. Using this, we characterize the measure expanding flows on a compact
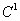 manifold via the notion of
manifold via the notion of
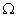 -stability. This is joint work with N. Nguyen.
-stability. This is joint work with N. Nguyen.
报告人简介:Keonhee Lee 教授现任教于韩国忠南国立大学数学系,其研究领域为动力系统的几何理论与遍历理论,具体方向有双曲理论(含伪轨跟踪理论、可扩性及结构稳定性等)、一致双曲性之外的大范围分析、可测动力性质以及符号动力系统等。迄今已在 J. Differential Equations、Discrete Contin. Dyn. Syst和Proc. Edinb. Math. Soc.等知名学术期刊上发表学术论文60余篇。Lee教授曾担任韩国数学会的副主席,现在也是期刊Journal of Korean Mathematical Society主编以及Dynamical Systems等期刊的编辑。
邀请人:文晓
