北航数学论坛学术报告
--- 分析与偏微分方程讨论班(2023春季第1、2、3讲)
Radial symmetry and monotonicity of solutions for fractional and dual fractional parabolic equations
陈文雄 教授
(美国Yeshiva大学)
时间与地点:
第一讲:4月3日(周一)8:00-10:00(北京时间),腾讯会议:621-946-189,链接:https://meeting.tencent.com/dm/QdASgoBAs34U
第二讲:4月6日(周四)8:00-10:00(北京时间),腾讯会议:764-921-188,链接:https://meeting.tencent.com/dm/YW7wruIyhJS6
第三讲:4月8日(周六)8:00-10:00(北京时间),腾讯会议:251-544-372,链接:https://meeting.tencent.com/dm/09ClvuUgvKOR
摘要: In this series of talks, we will consider ancient solutions for the fractional parabolic equations
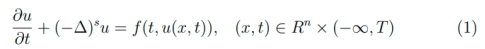
and entire solutions for the dual fractional parabolic problems
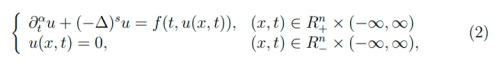
where
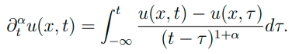
We will first introduce the main results in two of our recent papers (see the references below) and then illustrate the main ideas in applying the method of moving planes to establish radial symmetry of solutions for (1) and the monotonicity of solutions for (2).
It is worth mentioning that, for problem (2), the solutions are allowed to be unbounded, and we only assume
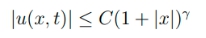
for some γ<2s. Due to the nonlocal nature of the derivative with respect to t, some approaches for equation (1) no longer work. We will explain how to circumvent these difficulties.
报告人简介: 陈文雄,Yeshiva大学数学系终身教授,南开大学特聘讲座教授,曾多次获得美国国家科学基金奖,致力于偏微分方程、非线性泛函分析和几何分析等领域研究。研究方向主要包括:非线性偏微分方程正解的分类、几何不等式和黎曼流形上PDE正解的性质等。论文发表在Annals of Math.、Duke Math. J.、J. Diff. Geom.、Comm. Pure Appl. Math.、Advances in Math.、Arch. Rat. Mech. Anal.等国际著名数学期刊,他引超5000次。
邀请人:戴蔚
欢迎大家参加!
