2020年10月29日上午，复旦大学研究员丁琪应基础数学系微分几何组老师的邀请，在微分几何组固定（每周四上午）的讨论班上为师生带来了一场题为“Minimal hypersurfaces in manifolds of Ricci curvature bounded below”的线上（腾讯会议）学术报告。报告由张世金老师主持。
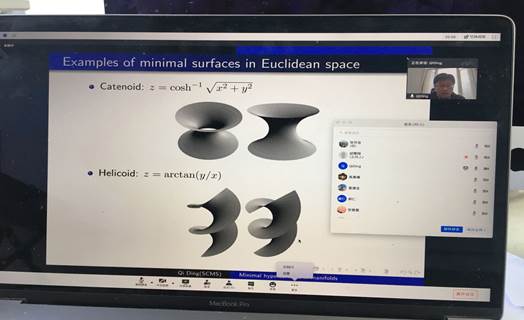
丁琪研究员在报告中首先回顾了流形中stationary varifold----可以看成是经典极小曲面的推广，并回顾了经典的Cheeger-Colding理论，介绍了他最近关于一串里奇曲率有下界的流形和极小超曲面分别对应的极限空间上的距离函数的Laplacian比较定理，作为此定理的应用，得到了两个有意思的结果。
此次线上报告吸引了学院的众多学生和国内同行的兴趣。报告结束后，几何组教师、同行专家积极与丁琪研究员进行了交流和热烈的讨论。报告持续了近两个小时。
丁琪，复旦大学上海数学中心青年研究员，2012年复旦大学博士毕业，然后到德国马克斯普朗克研究所做博士后，2014年入职复旦大学任教至今，2015年曾获钟家庆数学奖，2017年访问美国MIT一年，2019年获得国家优秀青年基金。研究方向：微分几何、偏微分方程、几何测度论。
首页
>>
新黄金城xhjc官方网站
>>
正文
